문제를 천천히 읽어보자.
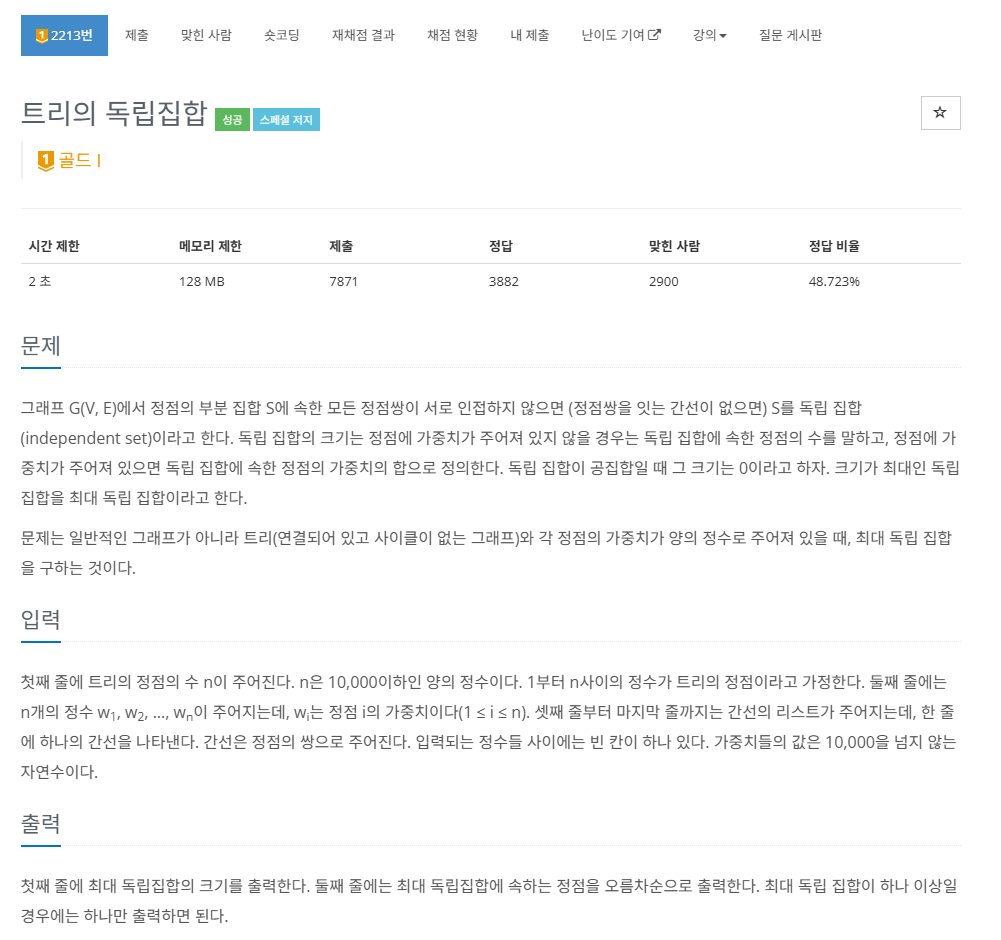
독립집합이란, 모든 정점 쌍이 인접하지 않은 정점들의 집합이라고 한다. 간단하게 그림을 그려보면, 다음과 같은 예시를 들 수 있다.

그리고 다음과 같은 애들은 독립집합이 아니다.
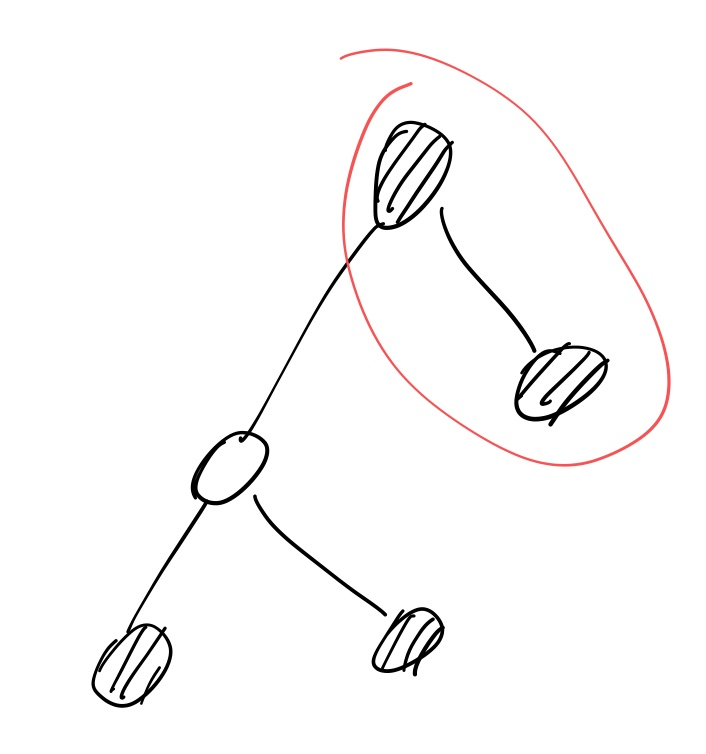
여기서 문제는 한가지 새로운 정의를 내린다.
독립집합의 크기란? 독립 집합 내 정점들의 가중치의 합
정점의 가중치는 정수로 주어지고, 10000 이하로 제한되어 있다.
우리의 목표는 독립집합을 이루는 경우의 수 중, 가장 큰 "집합 내 원소의 가중치의 합"을 구하는 것이다.
문제에 그래프 형태가 트리 구조로 되어있다고 하는데, 여기에서 우리는 중요한 관찰을 할 수 있다.
트리구조로 되어있다는 것은,
정점 A가 어떤 독립 집합 S에 포함/제외되는 것이 재귀적으로 자기 자신에게 영향을 주는 "사이클" 이 존재하지 않는다는 뜻이다.
따라서 우리는, 해당 정점의 포함/제외 여부를 "해당 정점에서 즉시 결정"할 수 있고, 이 때, 문제를 부분문제로 쪼개 풀 수 있게 된다.
만약 자기 자신을 포함시킨다면
자신의 자식 노드들을 "전부 제외했을 때"의 독립집합의 가중치의 합을 더해야 하고,
자기 자신을 제외시킨다면,
자신의 자식 노드들을 "포함하거나, 제외했을 때"의 독립집합의 가중치의 합을 더해야 한다.
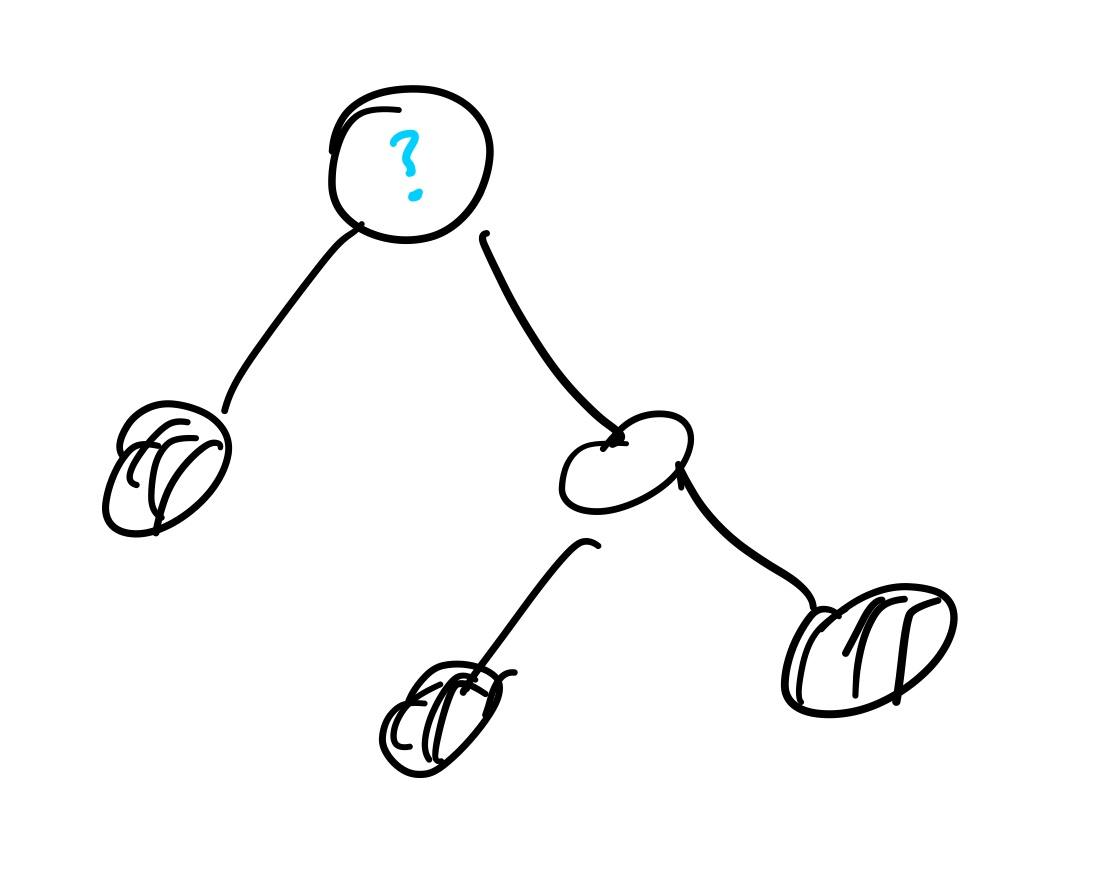
다음과 같이 계산하게 되면, 단순 DFS 에 DP를 얹은 형태인 Tree DP 문제가 되고, 임의의 노드를 Root로 잡고 재귀적으로 풀어나가게 되면 간단하게 해답을 구할 수 있게 된다.
(순회한 정점을 구하는 것은 단순 계산으로 봐도 O(2500만)을 넘기지 않으므로, 설명을 건너뛰도록 하겠다.)
#include <bits/stdc++.h>
#define ll long long
#define INF ((int)1e9 + 10)
#define lINF ((ll)1e18 + 10LL)
const ll MOD = 1000000007LL;
// #include <atcoder/modint.hpp>
// using mint = atcoder::modint998244353;
using namespace std;
vector<int> g[10001];
vector<int> visitList[10001][2];
int weight[10001];
int dp[10001][2];
void dfs(int now, int prev) {
dp[now][0] = 0;
dp[now][1] = weight[now];
visitList[now][1].push_back(now);
for (int i = 0; i < g[now].size(); i++) {
int next = g[now][i];
if (next == prev) continue;
dfs(next, now);
if (dp[next][0] > dp[next][1]) {
dp[now][0] += dp[next][0];
for (int j = 0; j < visitList[next][0].size(); j++) {
visitList[now][0].push_back(visitList[next][0][j]);
}
} else {
dp[now][0] += dp[next][1];
for (int j = 0; j < visitList[next][1].size(); j++) {
visitList[now][0].push_back(visitList[next][1][j]);
}
}
dp[now][1] += dp[next][0];
for (int j = 0; j < visitList[next][0].size(); j++) {
visitList[now][1].push_back(visitList[next][0][j]);
}
}
}
void Solve() {
int n;
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> weight[i];
}
for (int i = 0; i < n - 1; i++) {
int a, b;
cin >> a >> b;
g[a].push_back(b);
g[b].push_back(a);
}
dfs(1, 0);
int mxFlag = 0;
int mx = 0;
if (mx < dp[1][0]) {
mxFlag = 0;
mx = dp[1][0];
}
if (mx < dp[1][1]) {
mxFlag = 1;
mx = dp[1][1];
}
cout << mx << '\n';
sort(visitList[1][mxFlag].begin(), visitList[1][mxFlag].end());
for (int i = 0; i < visitList[1][mxFlag].size(); i++) {
cout << visitList[1][mxFlag][i] << ' ';
}
cout << '\n';
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
int T = 1;
while (T--) Solve();
return 0;
}
/*
찾아야 할 것들
1. int 오버플로우, out of bounds
2. 특수한 경우(n=1?)
3. 잘못된 가정 & 증명
*아무것도 하지 않는 대신 무언가를 수행하기. 체계적인 상태를 유지.
*적어두기 & 구하고자 하는 것의 계층 구조 표현 -> 정확히 & 입체적으로 파악
*한가지 접근 방식에 얽메이지 말기 -> 응용의 끝 알기
*/
// 알고리즘의 작동방식 "완전히" 이해하려 노력하기 -> 수식 & 그림화, 조건 정리
// 수행 목표
// 1. 아이디어 획득 : "추론"
// - 문제 알고리즘/특징의 "증명"으로 아이디어
// - {BruteForce, greedy, D&C, DP, graph, math}
// - 전체 알고리즘이 “결국 구하고자 하는 것” 놓치지 않기
// - “책임” 뽑아내기 -> 개념화, 정의, 추상화, 귀납적 사고
// - 각 기능들이 어떤 책임을 가지고 있는지
// - “어떤 패턴”으로 동작하는지
// - 가장 Naive한 상태/알고리즘부터 시작하기 (완전 탐색, 단순 자료구조)
// - 뚜렷한 증명이 나오지 않을 땐, 어떤 기준을 만들고 나눠서 보기
// - 뚜렷한 최적화 기법이 떠오르지 않을 땐, 문제에 주어진 특이한 특징을 잡기
// - 단위 동작의 조건 분기 파악
// - 가장 극단적인 경우에서 추론 (가장 차이가 뚜렷한 예제)
// 2. "처음"부터 직접 경우의 수 전개(수식&도식화, 엄밀한 조건 정리)
// - 알고리즘 내에 어떤 역할들이 있는지 -> 직접 들어가보기
// - 알고리즘 내에 어떤 기능들이 있는지 -> 직접 수행해보기
// - "끝까지 구체화"로 접근해야, "깔끔한 추상화"가 나온다.
// 3. cutting | 구현(차근차근 단순화 & 최적화)
/*
수학적 접근 방법
1. 불변성
2. 극단성
3. 홀짝성
4. 단조성
5. 선형성
6. 영역성
*/
/*
정당성 증명 방법
1. 귀납법 -> 결과값 만드는 점화식의 존재성을 증명하는 것
2. 귀류법 -> 결과값의 참/거짓을 가정하고 이전단계의 모순을 발견하여 증명
3. 경우에 의한 증명 -> 반례 찾기
4. 구성적 증명 -> 부분문제의 결과값을 만드는 원인를 분석하여 증명하는 방법
5. 비둘기집의 원리
6. 대각선 논법(연역법) -> A<C 이고 C<B 임을 이용해 A<B를 증명하는 방법
*/
/*
take notes.
// 다시 보는용이 아닌
// 현재의 흐름을 가장 잘 이어갈 수 있도록 !!!
*/
// commit 시 피드백할 것 Message로 남겨두기!!
// 틀리면 느낌표 추가하기'PS > Baekjoon OJ' 카테고리의 다른 글
| [9376] 탈옥 (0) | 2025.03.29 |
|---|---|
| [1475] 방 번호 (0) | 2024.12.03 |
| [2577] 숫자의 갯수 (0) | 2024.12.03 |